
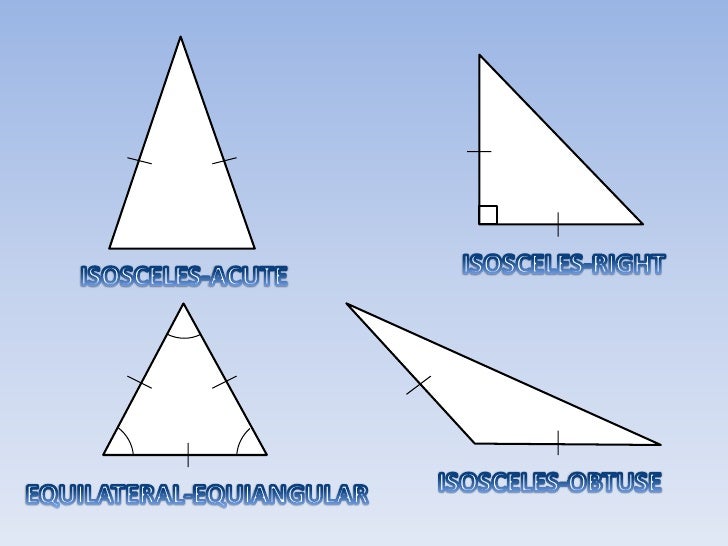

With the Law of Cosines, there is also no problem with obtuse angles as with the Law of Sines because the cosine function is negative for obtuse angles, zero for right, and positive for acute angles. Then such a triangle is called an obtuse isosceles triangle which would be of a. One example of isosceles obtuse triangle angles is 30, 30, and 120. Isosceles obtuse triangles are triangles that have two sides of the same length and an angle greater than 90 degrees. Obtuse Triangle- A triangle whose any one angle is obtuse angle is called an obtuse. Isosceles obtuse triangle: An isosceles obtuse triangle is a triangle in which one of the three angles is obtuse (lies between 90 degrees and 180 degrees), and the other two acute angles are equal in measurement. Suppose, we have a triangle, ABC where AB BC and ABC > 90 o. It follows Pythagorean theorem, which you can study here. angle, angles, degrees, Degree, isosceles triangle, isosceles triangles, obtuse triangle. It is best to find the angle opposite the longest side first. A triangle is said to be an obtuse isosceles triangle if apart from two sides being equal, one of the angles of the triangle is an obtuse angle, i.e. An isosceles triangle with angles 145, 17.5, 17.5. Pythagorean theorem is a special case of the Law of Cosines and can be derived from it because the cosine of 90° is 0. Pythagorean theorem works only in a right triangle. The Law of Cosines extrapolates the Pythagorean theorem for any triangle. The cosine rule, also known as the Law of Cosines, relates all three sides of a triangle with an angle of a triangle. Calculation of the inner angles of the triangle using a Law of CosinesThe Law of Cosines is useful for finding a triangle's angles when we know all three sides. T = 2 a h a h a = a 2 T = 5 2 ⋅ 1 2 = 4. An obtuse isosceles triangle is one in which the apex angle is obtuse and the other two angles are equal and acute.


 0 kommentar(er)
0 kommentar(er)
